How to format a given array (matrix) in spiral form (snail or clockwise spiral sorting) in Python

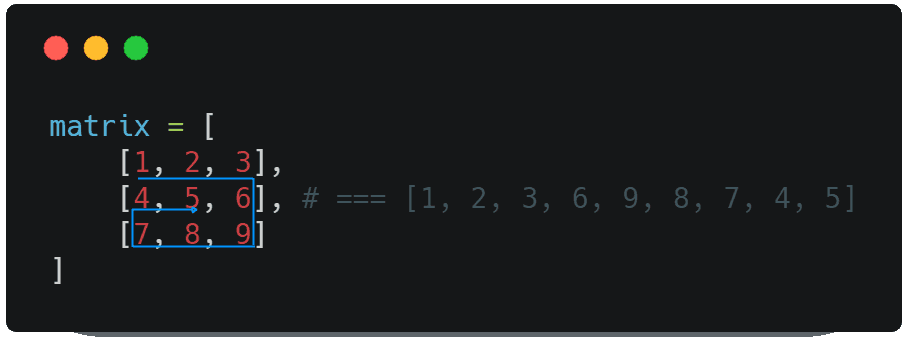
Although you wont probaly absolutely never use something like this in your Job, because, it doesn't make sense at all, this exercise is very common for homework of young programmers. The idea is simple but the way to achieve not so much, you will have an array that has multiple arrays inside with a square or rectangular shape in the rough sense of the word and the task is to create a function that returns an array with single items that follow the order of a spiral form or well known as a snail as well, for example, analyze the following examples and expected results:

# Example 1.
matrix = [
    [1, 2, 3],
    [4, 5, 6], 
    [7, 8, 9]
]
# Expected = [1, 2, 3, 6, 9, 8, 7, 4, 5]
print some_function(matrix)

# Example 2.
matrix = [
    [1,  2 , 3,  4,  5 ],
    [6,  7 , 8 , 9,  10], 
    [11, 12, 13, 14, 15],
    [16, 17, 18, 19, 20]
]             
# Expected = [1, 2, 3, 4, 5, 10, 15, 20, 19, 18, 17, 16, 11, 6, 7, 8, 9, 14, 13, 12]
print some_function(matrix)

If you still don't get it, see the graphical explanation in the image of this article, where you can see the arrow following the structured array with the shape of a snail.

Implementation

The given structure will always be a single array with multiple arrays inside, so you can work with it as a quadratic object iterating all over every row and using some flags to return to every row according to the status of the generated array:

"""
Given a matrix of m x n elements (m rows, n columns),
return all elements of the matrix in spiral order.
For example,
Given the following matrix:
[
 [ 1, 2, 3 ],
 [ 4, 5, 6 ],
 [ 7, 8, 9 ]
]


It should return [1,2,3,6,9,8,7,4,5].
"""
def spiral_traversal(matrix):
    res = []
    if len(matrix) == 0:
        return res
    row_begin = 0
    row_end = len(matrix) - 1
    col_begin = 0
    col_end = len(matrix[0]) - 1

    while row_begin <= row_end and col_begin <= col_end:
        for i in range(col_begin, col_end+1):
            res.append(matrix[row_begin][i])
        row_begin += 1

        for i in range(row_begin, row_end+1):
            res.append(matrix[i][col_end])
        col_end -= 1

        if row_begin <= row_end:
            for i in range(col_end, col_begin-1, -1):
                res.append(matrix[row_end][i])
        row_end -= 1

        if col_begin <= col_end:
            for i in range(row_end, row_begin-1, -1):
                res.append(matrix[i][col_begin])
        col_begin += 1

    return res

With this function you will be able to structure the original array with the desired form:

mat = [
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]
]

# [1, 2, 3, 6, 9, 8, 7, 4, 5]
print(spiral_traversal(mat))

Happy coding !