In mathematics, Pascal's triangle is a triangular arrangement of numbers that gives the coefficients in the expansion of any binomial expression, such as (x + y)n. It is named for the 17th-century French mathematician Blaise Pascal. As an easier explanation for those who are not familiar with binomial expression, the pascal's triangle is a never-ending equilateral triangle of numbers that follow a rule of adding the two numbers above to get the number below.
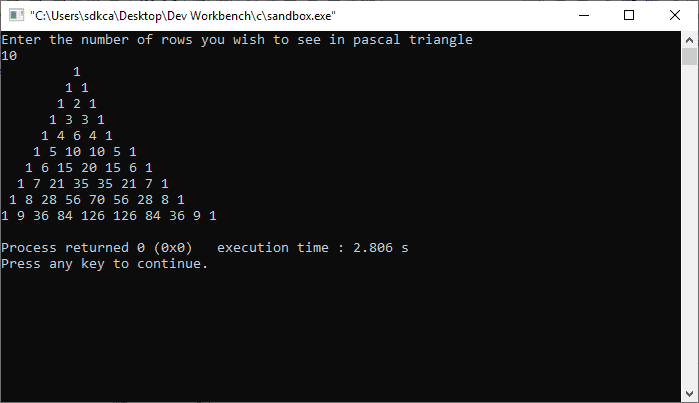
In this article, we'll show you how to generate this famous triangle in the console with the C programming language.
Implementation
Graphically, the way to build the pascals triangle is pretty easy, as mentioned, to get the number below you need to add the 2 numbers above and so on:
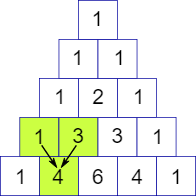
With logic, this would be a mess to implement, that's why you need to rely on some formula that provides you with the entries of the pascal triangle that you want to generate. The easiest way to do it in programming is with the usage of Binomial coefficient or the well known "n choose k":
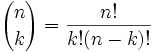
The following code works like this: the user will be prompted for a number that defines the number of rows that the triangle should have, the first for loop will iterate the number of times that the user provides. On every iteration, another 2 loops will be executed, the first one defines the number of spaces from left to the right, removing one of those spaces on every iteration until the last row, that shouldn't have any space and the important loop that prints the value of the corresponding number with the mentioned formula:
#include <stdio.h>
long factorial(int);
int main()
{
int i, n, c;
printf("Enter the number of rows you wish to see in pascal triangle\n");
scanf("%d",&n);
for (i = 0; i < n; i++)
{
for (c = 0; c <= (n - i - 2); c++){
printf(" ");
}
for (c = 0 ; c <= i; c++){
printf("%ld ", factorial(i)/(factorial(c)*factorial(i-c)));
}
printf("\n");
}
return 0;
}
// See our implementation of factorial for more information
// https://ourcodeworld.com/articles/read/857/how-to-get-the-factorial-of-a-number-in-c
long factorial(int n)
{
int c;
long result = 1;
for (c = 1; c <= n; c++){
result = result*c;
}
return result;
}The advantage of this approach is that you will really see an equilateral triangle, not a triangle rectangle which looks a lot better on the output, besides increases the difficulty of the exercise. Is worth to mention that we use the factorial approach that we wrote on a previous article.
Happy coding !