How to calculate an approximation of Pi (π) with JavaScript (Solution for Programming Interview Question)

In the last days I solved another of those tedious interview assignments when you apply for a new job. In this case, the exercise was new for me and is the following one. In this exercise we will calculate an approximation of π (Pi).

The technique is as follows: Take a random point P at coordinate X, Y such that 0 <= x <= 1 and 0 <= y <= 1. If x2 + y2 <= 1, then the point is inside the quarter disk of radius 1, otherwise the point is outside.

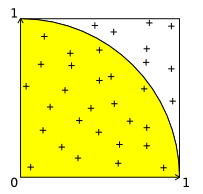
We know that the probability that the point is inside the quarter disk is equal to π/4. You need to write the method approx(pts) that will use the array of points pts to return an approximation of the number Pi (π).

• Each item in pts is a point.
• A point is represented by an array containing exactly 2 numbers, respectively x and y such that 0 <= x <= 1 and 0 <= y <= 1.
• pts is never null and always contains at least one item.

In this article, I will share with you a possible solution for this problem using a Monte Carlo simulation with JavaScript.

Solution

So, let's get started with the basics. The exercise mentions the approx function that we need to create and receives the pts argument that is generated randomly, specifically by a code like the following one:

let pts = [];

for(let i = 0;i < 10000; i++){
    let x = Math.random();
    let y = Math.random();

    pts.push([x, y]);
}

// pts contains an array like the following one:
// Where the index 0 of the array is X 
//       and index 1 of the array is Y
//[
//    [
//        0.6265471354441587,
//        0.019122543122902957
//    ],
///   [
//        0.9676467567764127,
//        0.9941570823210109
//    ],
//    [
//        0.828985078753246,
//        0.34295195222317565
//    ],
//
//...
//

console.log(pts);

So, that's the argument that the approx function will receive, we need to work with this data. Now that we understand this, we need to find a way to calculate the value of Pi. Most of the developers will see this task a little bit confusing and problematic, however if you research enough, you will find the solution. In this case, it's possible to calculate the value of Pi using random numbers, using a Monte Carlo Simulation.

The theory is quite impressive and takes a little time to understand it totally, so I really recommend you to read the article for a detailed explanation.

We know that the probability that the point is inside the quarter disk is equal to π/4, so from the data that we have of the random numbers, we need to determine the number of points that satisfy the condition x2 + y2 <= 1, and the number of points of the dataset.

Pi is going to be equals to 4 multiplied by the quotient of the division between the number of points that satisfy the condition and the number of points of the dataset, providing an approximate value of PI, for example with 8 of the 10 points, we will obtain a value close to PI:

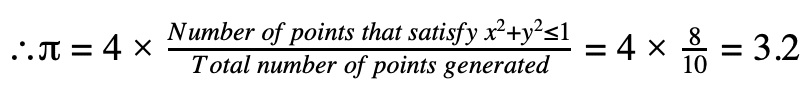
For the implementation in JavaScript, considering the values of PTS that in this case are 10.000 values, the function that solves this problem is the following one:

function approx(pts){
    let pointsThatSatisfyTheFormula = [];

    for(let i = 0; i < pts.length;i++){
        let point = pts[i];
        let x = point[0];
        let y = point[1];

        if(Math.pow(x, 2) + Math.pow(y, 2) <= 1){
            pointsThatSatisfyTheFormula.push(point);
        }
    }

    let approximateValueOfPi = 4 * (pointsThatSatisfyTheFormula.length / pts.length);

    return approximateValueOfPi;
}

When executing the approx function providing a dataset as specified in the problem will always return a numeric value that is very close to PI.

Happy coding ❤️!